AMMM:Metadynamics
What is Metadynamics?
•A simulation method normally applied as part of molecular dynamics
•Used to estimate free energy and state functions of systems where ergodicity (given enough time simulation will explore all possible configurations/areas of phase space) is hindered by energy landscape
•Similar to: Adaptively biased MD, Adaptive reaction coordinate forces, Local elevation umbrella sampling
•Suggested and developed by Alessandro Laio and Michele Parrinello
How does Metadynamics work?
•Filling free energy wells with computational sand
•Tracking grains of sand placed along collective variables
•Eventually the wells are completely full and you add sand to sand (known as convergence)
•The landscape is opposite of sum of all sand
Movie: https://www.youtube.com/watch?v=IzEBpQ0c8TA
How Metadynamics Really Work!
•Collective variables (s): set of variables which accurately describe the system
•CV Examples: Dihedral angle for cis to trans butane, Distance for cation and anion
•Limitations: 3CV or 8CV with multiple replicas coupled together
•Exponential cost increase with each CV
•Grains of sand are bias potentials
•Hamiltonian is augmented with bias potential Vbias shown in Equation 1
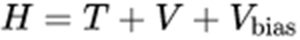
•Bias potential Vbias is continuously updated by adding bias (more grains of sand) visualized in Figure 1
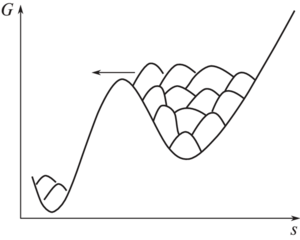

Defined Variables for Equation 2:
•Vbias: bias potential
•tsim: simulation time
•s: collective variable
•st: instantaneous collective variable at time t
•ω: bias deposition rate
•F: free energy
•C: constant (irrelevant)
•Evaluating the integral of bias potential over the time duration of the simulation returns free energy F with a negative sign given enough time
How to make Metadynamics efficient and computationally viable?
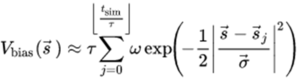
•Time is discretized into T time intervals
•The Dirac delta function is replaced with a Gaussian function
•Time intervals (T), bias deposition rate (ω), and width of Gaussian functions (σ) are constants determined as inputs
•Vbias equation for efficient implementation shown in Equation 3
Two types of Metadynamics
•Everything so far has been “original” or “plain” metadynamics
•Well-tempered metadynamics scales Gaussian height down as wells are filled
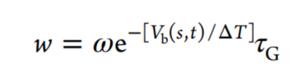
Defined Variables for Equation 4 and 5:
•w: Gaussian height
•ω: bias deposition rate
•Vb: estimate of free energy at current CV position and time step
•ΔT: tunable parameter controls how quickly Gaussian height reduces as wells are filled
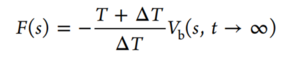
•F: free energy
•Final value of biasing potential is a scaled approximation of free energy as shown in Equation 5
• Well-tempered metadynamics allows for rapid exploration of phase space as the wells are filled quickly (at Vbias=0 the amount of bias deposited is relatively large, at Vbias=infinity the amount of bias deposited is infinitely small)
•As wells fill progressively smaller perturbations to bias potential lead to "smooth convergence" (less excess bias potential or sand deposited on 'top')
•Suggested and developed by Alessandro Barducci, Giovanni Bussi, and Michele Parrinello
Movie Comparing MD, MTD, and WTMTD: https://www.youtube.com/watch?v=IzEBpQ0c8TA
Applications of Metadynamics
•Able to sample free energy curve even when ergodicity is limited by energy landscape
•Keys to successful metadynamics simulation are choice and definition of CVs
•Applicable systems: Protein folding, Molecular docking, Phase transitions, Chemical reactions, Simple to complex systems as long as CVs are sufficient to describe system
•Widely integrated as PLUMED and Collective Variable Module:
•PLUMED: AMBER, GROMACS, LAMMPS, NAMD, Q ESPRESSO, CP2K, OpenMM
•Collective Variable Module: LAMMPS, NAMD, GROMACS, ORAC, CP2K, Desmond