Ammm:Mm mpole

Is electrostatic important?

All forces are electrostatic in nature.

Buckingham, Advances in Chemical Physics, 12, 107-142 (1967)

https://doi.org/10.1002/9780470143582.ch2

There is now general agreement that the significant forces between atoms and molecules have an electric origin. It is true that other sources exist, such as magnetic and gravitational interactions, but these can normally be neglected. When the molecules are far apart and the separation is large compared to the dimensions of the~molecules, the interaction energy is determined by the permanent electric moments, and their interactions comprise the electrostatic energy. The permanent moments produce a field that distorts the electronic structures of neighboring molecules leading to an additional interaction, the induction energy.

point charges

Atomic charges are not physical observables. Molecular charges, electrostatic potential and field are.

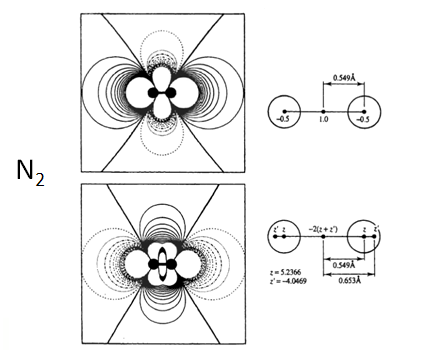
Nitrogen molecule: what would be the atomic charge?

Multipole expansion

Ref: https://en.wikibooks.org/wiki/Mathematical_Methods_of_Physics/The_multipole_expansion

${{M}_{i}}={{\left[{{q}_{i}},{{d}_{ix}},{{d}_{iy}},{{d}_{iz}},{{Q}_{ixx}},{{Q}_{ixy}},{{Q}_{ixz}},{{Q}_{iyx}},{{Q}_{iyy}},{{Q}_{iyz}},{{Q}_{izx}},{{Q}_{izy}},{{Q}_{izz}}\right]}^{T}}$

 

• monopole, i.e. point charge or zeroth moment of charge distribution
• dipole, or first moment of the charge distribution

   (-) -> (+) is a dipole vector
  A point dipole is adipole at the limit of separation approaches zero.
  carbon dioxide: 0 (Debye)
  carbon monoxide: 0.112
  water vapor: 1.85
  water in liquid: 2.8
  potassium bromide: 10.41

• quadrupole, second moment

quadrupole

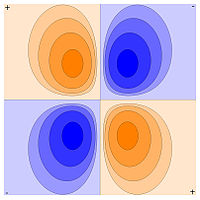
The traceless Cartesian quadrupole moment tensor of a charge distribution

$Q_{ij}=1/2\sum _{n}q_{n}(3x_{i}x_{j}-r^{2}\delta _{ij})\ ,$

or in tensor form:

quadrupole tensor

Traceless q tensor

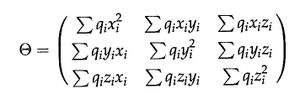
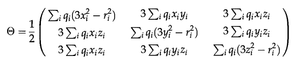
for a discrete system with individual charges q_n, or

$Q_{ij}=1/2\int \,\rho (x)(3x_{i}x_{j}-r^{2}\delta _{ij})\,d^{3}x\ ,$

for a continuous system with charge density ρ(x).

• Cartesian multipole expansion of a charge distribution:

Local frame definition

More detailed tutorials on multipole local frames (need to merge later):

https://biomolmd.org/mw/index.php/Tutorials:localframe

Vector and tensor values depend on the specific frames used.

In amoeba.prm, water multipole values are defined for O (type 22) and H (23) atoms:

multipole    22   23  -23             -0.51966
                                     0.00000    0.00000    0.14279
                                     0.37928
                                     0.00000   -0.41809
                                     0.00000    0.00000    0.03881
multipole    23   22   23              0.25983
                                    -0.03859    0.00000   -0.05818
                                    -0.03673
                                     0.00000   -0.10739
                                    -0.00203    0.00000    0.14412

Types of frames:

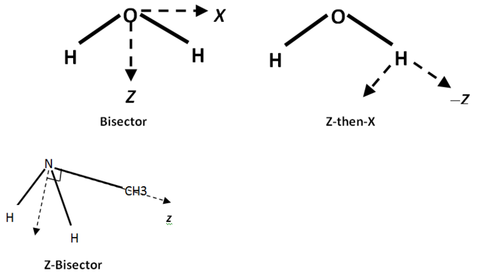
• Z-then-X is the most common.
• Bisector for atoms like O in H2O. Note this requires dx=dy=0, Qxy=Qyz=0
• z-then-bisector is used for N in methyl amine, where Z is C and H-N-H bisector is used to define X. Note that it is necessary that dy=0, Qxy=Qyz=0
• z only (22 0 0) can be used for N in N2. In this case, the atom will have dx=dy=0, Qxx=Qyy=-1/2Qzz (traceless), and Qxy=Qyz=Qxz=0

For example, the C in methanol, you can use Z only:
C_AT  0  0 
Or you can use z-then-x:
xxx  O_AT  HO_AT
where HO_AT is the hydroxyl hydrogen atom type. So atoms that not immediately connected is also allowed!

Many examples can be found in tinker/param/amoeba09.prm

In kmpole.f, you can find how tinker decide which frame is used by checking the sign and how many frame defining atoms there are:

              #type   kz_type    kx_type   ky_type_if_needed
              if (kz.ne.0 .and. kx.eq.0)  axt = 'Z-Only'
              if (kz.lt.0 .or. kx.lt.0)  axt = 'Bisector'
              if (kx.lt.0 .and. ky.lt.0)  axt = 'Z-Bisect'
              if (max(kz,kx,ky) .lt. 0)  axt = '3-Fold'

You can convert the atomic multipoles from one frame to another (your choice) using poledit.x

Some notes about local frames here: AMOEBA Multipole Local Frames

Spherical multipoles

Multipole can also be obtained by expanding in Legendre polynomial, instead of Taylor expansion. The potential due to a point charge can be expanded:

Spherical multipoles

$\Phi (r,\theta )\propto {\frac {1}{R}}={\frac {1}{\sqrt {r^{2}+a^{2}-2ar\cos \theta }}}.$

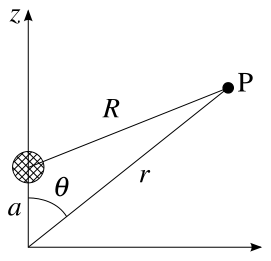
If r > a :$\Phi (r,\theta )\propto {\frac {1}{r}}\sum _{k=0}^{\infty }\left({\frac {a}{r}}\right)^{k}P_{k}(\cos \theta )$

if r < a :$\Phi (r,\theta )\propto {\frac {1}{r}}\sum _{k=0}^{\infty }\left({\frac {r}{a}}\right)^{k}P_{k}(\cos \theta )$

The same conclusion can be arrived at by solving the electric potential according to Laplace equation, $\nabla ^{2}\Phi (\mathbf {x} )=0$, by separation of variables. The solution takes the form of

$\Phi (r,\theta )=\sum _{\ell =0}^{\infty }\left[A_{\ell }r^{\ell }+B_{\ell }r^{-(\ell +1)}\right]P_{\ell }(\cos \theta ).$

$A_{\ell }$ and $B_{\ell }$ depend on the boundary conditions - Jackson, J.D. Classical Electrodynamics, 3rd edition, Wiley & Sons, 1999. page 103

A more detailed derivation of potential in spherical form for a point charge embedded in a dielectric sphere 
can be found in  When the dielectric inside and outside the sphere ε = 1, the equation reduce to gas-phase potential. 
click for pdf

You may see the potential expressed in the spherical harmonics or associated Legendre. The Legendre polynomial can be expressed in associated Legendre polynomial according to the addition theorem (cos(θ' − θ) = cosθ'cosθ + sinθsinθ')

Consider two unit vectors x and y, having spherical coordinates (θ,φ) and (θ′,φ′), respectively. The addition theorem states $P_{\ell }(\mathbf {x} \cdot \mathbf {y} )={\frac {4\pi }{2\ell +1}}\sum _{m=-\ell }^{\ell }Y_{\ell m}^{*}(\theta ',\varphi ')\,Y_{\ell m}(\theta ,\varphi ).$

where P_ℓ is the Legendre of order ℓ. This expression is valid for both real and complex harmonics.This is valid for any orthonormal basis of spherical harmonics of degree ℓ.

The spherical harmonics $Y_{\ell m}^{*}(\theta ',\varphi ')\,$(angular portion of a set of solutions to Laplace's equation) are related to the associated Legendre polynomial: $Y_{\ell }^{m}(\theta ,\varphi )={\sqrt {{(2\ell +1) \over 4\pi }{(\ell -m)! \over (\ell +m)!}}}\,P_{\ell }^{m}(\cos {\theta })\,e^{im\varphi }$

Further reading: http://en.wikipedia.org/wiki/Spherical_harmonics

Why use higher order moments at atoms

Example I: Using atomic partial charge only is inadequate to give an accurate representation of electrostatic potential.

Electrostatic Potential by Atomic Multipoles

	Relative Error (%)
Molecule	Monopole Only	Monopole+Dipole	M+D+Q
Methane	13.53	1.04	0.39
Water	8.44	0.88	0.01
Ammonia	9.90	2.31	0.02
Methanol	8.35	1.31	0.02
Acetylene	1.34	0.06	0.02
Formamide	3.68	0.65	0.03
Methyl Acetate	6.03	0.67	0.02
DiMe Amine	16.27	1.48	0.03
NMA	3.26	0.30	0.01

Example II: HBond confiiguration

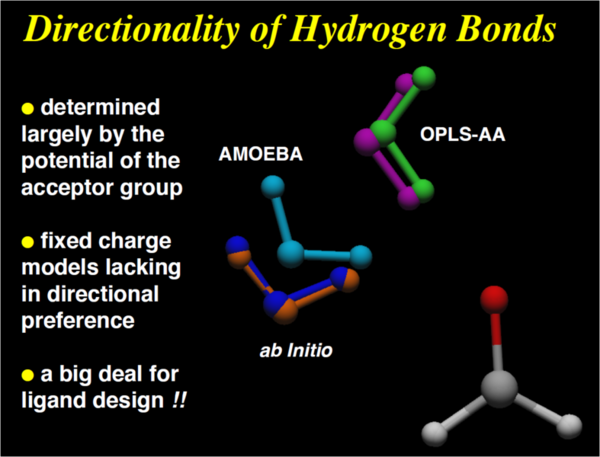
How to derive permanent multipoles

DMA

Distributed Multipole Analysis allows to derive atomic multipoles from ab initio calculations.

Original DMA is described in and . The original DMA (explained in Estar manual below) works well for small molecule without diffuse function in the basis set. Stone improved the basis set dependence of DMA values, using a grid based quadrature for partitioning the contributions to the charge density from diffuse basis functions. The DMA from this new procedure however is not as transferable as the original one among conformations.

In Stone's latest GDMA program v2.2, the original DMA procedure is invoked by setting "switch=0".

Now we use the original DMA with a small basis set (MP2/6-311G**), and then optimize the DMA to higher level electrostatic potential on a grid (MP2/6/311++G2d,dp or aug-cc-pvtz) using "potential" program in TINKER. For flexible molecules, multiple conformations (e.g. local minima of alanine dipeptide) are used in the fitting.

Estar explains how DMA works:

Cumulative Atomic Multipole Moments (CAMM)

Explained above

AIM (Bader)

The theory of Atom In Molecule dissects molecules into atoms based on the topology of electron density. The main features are:

• A molecule can be uniquely divided into a set of atomic volumes. These volumes are divided by a series of surfaces through which the gradient vector field of the electron density has no flux. Atomic properties such as atomic charge, dipole moment, and energies can be calculated by integrating their corresponding operators over the atomic volume.
• Two atoms are bonded if their atomic volumes share a common interatomic surface, and there is a (3, −1) critical point on this surface. A critical point is defined as a point in space where the gradient is zero. A (3, −1) critical point is defined as a critical point at which two of the eigenvalues of the Hessian matrix at the critical point are negative, while the other eigenvalue is positive. In other words, a bonding critical point is a first-order saddle point in the electron density scalar field. A bond path is the line along which the electron density is a maximum with respect to a neighboring line. Along the associated virial path the potential energy is maximally stabilizing.
• The interatomic bonds are classified as either closed shell or shared, if the Laplacian of the electron density at the critical point is positive or negative, respectively.
• Geometric bond strain can be gauged by examining the deviation of the bonding critical point from the interatomic axis between the two atoms. A large deviation implies larger bond strain.

Reading and software: 
http://www.chemistry.mcmaster.ca/bader/aim/ 
http://en.wikipedia.org/wiki/Atoms_in_molecules

Multipole interaction energy

In the Cartesian Polytensor formalism,Applequist, J.,Journal of Mathematical Physics, 24 736-741 (1983), Applequist, J. Phys. A: Math. Gen. 22 (1989) 4303-4330. Yong Kong, Multipole Electrostatic Methods for Protein Modeling with Reaction Field Treatment, Molecular Biophysics Program, Washington University, St. Louis, August 1997 http://dasher.wustl.edu/ponder/papers/kong-thesis.pdf the interaction energy between atoms i and j separated by rji is represented as

$U_{ele}^{perm}(ij)=M_{i}^{T}{{T}_{ij}}{{M}_{j}}$

Mike Kong's thesis is a well written source for understanding these formula. 
PDF is available in the references at the bottom of the page.

or in expanded form as

$U_{ele}^{perm}(ij)={{\left[{\begin{matrix}{{q}_{i}}\\{{\mu }_{ix}}\\{{\mu }_{iy}}\\{{\mu }_{iz}}\\{{Q}_{ixx}}\\\vdots \\\end{matrix}}\right]}^{t}}\left[{\begin{matrix}1&{\frac {\partial }{\partial {{x}_{j}}}}&{\frac {\partial }{\partial {{y}_{j}}}}&{\frac {\partial }{\partial {{z}_{j}}}}&\cdots \\{\frac {\partial }{\partial {{x}_{i}}}}&{\frac {{\partial }^{2}}{\partial {{x}_{i}}\partial {{x}_{j}}}}&{\frac {{\partial }^{2}}{\partial {{x}_{i}}\partial {{y}_{j}}}}&{\frac {{\partial }^{2}}{\partial {{x}_{i}}\partial {{z}_{j}}}}&\cdots \\{\frac {\partial }{\partial {{y}_{i}}}}&{\frac {{\partial }^{2}}{\partial {{y}_{i}}\partial {{x}_{j}}}}&{\frac {{\partial }^{2}}{\partial {{y}_{i}}\partial {{y}_{j}}}}&{\frac {{\partial }^{2}}{\partial {{y}_{i}}\partial {{z}_{j}}}}&\cdots \\{\frac {\partial }{\partial {{z}_{i}}}}&{\frac {{\partial }^{2}}{\partial {{z}_{i}}\partial {{x}_{j}}}}&{\frac {{\partial }^{2}}{\partial {{z}_{i}}\partial {{y}_{j}}}}&{\frac {{\partial }^{2}}{\partial {{z}_{i}}\partial {{z}_{j}}}}&\cdots \\\vdots &\vdots &\vdots &\vdots &\ddots \\\end{matrix}}\right]\left({\frac {1}{{r}_{ji}}}\right)\left[{\begin{matrix}{{q}_{j}}\\{{\mu }_{jx}}\\{{\mu }_{jy}}\\{{\mu }_{jz}}\\{{Q}_{jxx}}\\\vdots \\\end{matrix}}\right]$

Note the multipoles above are in global frame. The multipoles are defined in local frame in the parameter files. At every energy and force evaluation, the multipoles are rotated from local frame to the global frame. ${{M}_{local}}={{\Re }^{-1}}M$

For TINKER implementation of Ewald summation of multipole interaction energy, force, and torque see this paper (see Smith CCP5 paper)

Polarization effect

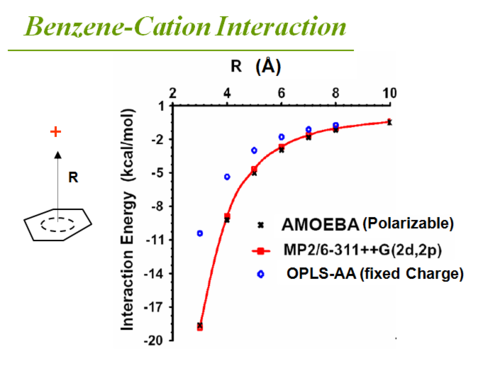
Cation - pi interaction

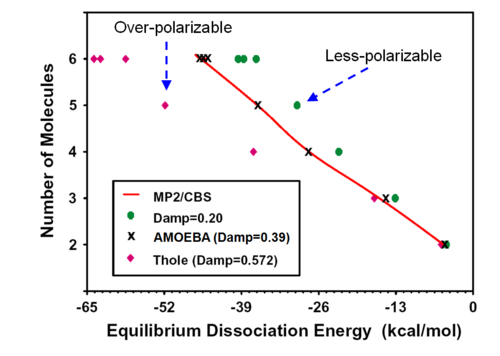
Water cluster association energy

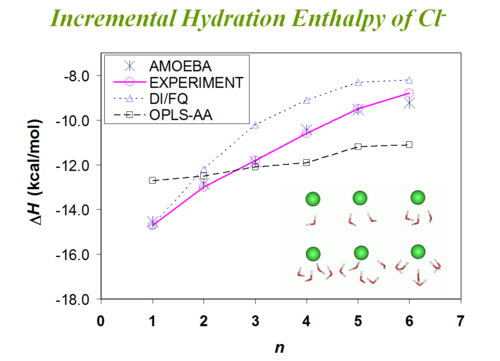
Water-Chloride binding enthalpy

Selected pages from Stone book on SAPT, distributed polarizabilities.

Induced dipole

Interactive polarizability model:

${{\mu }_{i}}={{\alpha }_{i}}\left(\sum _{j\neq i}{T_{ij}^{1}{{M}_{j}}}+\sum _{k\neq i}{T_{ik}^{11}{{\mu }_{k}}}\right)$ and

$U_{ele}^{ind}=-{\frac {1}{2}}{{\left({{\mu }^{ind}}\right)}^{T}}E\,$ where $E\,$ is the permanent field.

1/2 is a result of balance between energy cost of creating induced dipoles and energy gain from induced dipole interactions 

$T_{ij}^{1}=\left[{{\nabla }^{1}},{{\nabla }^{2}},{{\nabla }^{3}},...\right]$ is a 3 × 13 matrix with ${{\nabla }^{l+m+n}}={\frac {{\partial }^{l}}{\partial {{x}^{l}}}}{\frac {{\partial }^{m}}{\partial {{y}^{m}}}}{\frac {{\partial }^{n}}{\partial {{z}^{n}}}}$ representing the second through fourth rows of the matrix T. $T_{ik}^{11}=\nabla _{ik}^{2}$ a 3×3 sub matrix, consists of elements in corresponding to the dipole moments. The atomic polarizability is isotropic. The off-diagonal elements the tensor, αi , are all zero and a single value for all three diagonal elements. Note that the effect of any permanent field on the induced dipole is additive.

Iterative solution with successive over-relaxation (SOR).

$\mu _{i}^{}(n+1)=(1-\omega )\mu _{i}^{}(n)\,\,+\,\,\omega \,\,\left[\mu _{i}^{}(0)+{{\alpha }_{i}}\sum _{\{k\}}{T_{ik}^{11}\,\mu _{k}^{}(n)}\right]$

ω needs to be bigger than 0,5, typically 0.7.

α is the atomic isotropic polarizability.

• Atomic polarizability is not a physical quantity but molecular polarizability is an observable.
• The key of an empirical polarizability model is to reproduce the (QM or experimental) molecular response.
• Interactive (Applequist) -- use small atomic polarizability; no damping

• Applequist is the first to use distributed atomic polarizability, to empirically compute CD spectrum and other optical properties of peptides.

• He also proposed a model that combine induced dipole and charges together.

• Additive model (Dykstra)-- requires each atom has a polarizability tensor

• Interactive (Thole) -- use damping. Provide better anisotropy in molecular response than Applequist model.

• A good review that compares above by Dykstra

About damping in polarization

We use "damping" to modulate polarization strength and avoid polarization catastrophe (induced dipoles do not converge, go to infinity during self consistent iteration).

Physically the damping is replacing point charge/multipoles with smeared distribution. Mathematically the damping is is multiplying Coulomb potential/field with exp function: 1/r - > (1-exp[a*u^3)...)/r) above

The damping coefficient "a" goes into the exponent. smaller "a" means stronger damping.

AMOEBA assign each atom a polarizability and a damping coeff "a", 99% time a=0.39. See "Polarize xxx " in prm file For some divalent ions, we used smaller than 0.39. In Tinker energy and force calculations, when two atoms polarize each other and each has own/different "a", we use the smaller one. So for the divalent ion -water (or anything else), the smaller "a" is used. This is why most time, we do not use "a" > 0.39. If we do, only that atom interacting with its own type will use this bigger "a", every other pair uses 0.39 or smaller.

When you optimize "a" for lanthanides -water , try to keep "a" <= 0.39 . Bigger values has no effect (since water O and H have 0.39) and numerical gradient wrt to "a" will be broken

Polarization group and Intramolecular polarization

Polarization occurs intramolecularly as well as intermolecularly.

A large molecule can be divided into (functional) groups, the permanent multipoles will polarize each other like small molecules would do to each other. The multipole derived from ab initio calculations for the above molecule would however include the intramolecular polarization already.

Starting from the ab initio atomic multipoles (DMA) for an arbitrary conformer of a model compound, , one can derive the intrinsic “permanent” atomic multipole moments (PAM), , that satisfy

$M_{i}^{DMA}=M_{i}^{}+{{\mu }_{i}}$

where μi is the dipole induced by intramolecular polarization of Mi. The Mi is obtained by an iterative procedure similiar to above. This approach provides a route to derive multipole parameters from larger model compounds with intramolecualr polarization. We have previously shown that the combination of one set of permanent {Mi} and conformation-dependent induced dipole{µi} moments is able to reproduce the QM electrostatic potential of flexible molecules at various conformations.

Induction Energy

Recall Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{ele}^{ind}=-\frac{1}{2}{{\left( {{\mu }^{ind}} \right)}^{T}}E} or in pairwise Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{ele}^{ind}=-\frac{1}{2}\sum_{i}^{{}}{{{\left( \mu _{i}^{ind} \right)}^{T}}{{E}_{i}}}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle E \,} is the permanent field.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left( {{\alpha }^{-1}}-{{T}^{11}} \right){{\mu }^{ind}}={{T}^{1}}M=E}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle C = \left( {\alpha}^{-1}-{T}^{11}\right)}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{ele}^{ind}=-\frac{1}{2}{{\left( {{\mu }^{ind}} \right)}^{T}}E=-\frac{1}{2}{{E}^{T}}{{C}^{-1}}E}

Force and gradient

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{x,i}=-\frac{\partial U^{ind}_{system}}{\partial x_{i}}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle U_{sys}^{ind}=-\frac{1}{2}{{\left( {{\mu }^{ind}} \right)}^{T}}E=-\frac{1}{2}{{E}^{T}}{{C}^{-1}}E}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial U_{sys}^{ind}}{\partial {{x}_{k}}}=-\frac{1}{2}\left( \frac{\partial {{E}^{T}}}{\partial {{x}_{k}}}{{C}^{-1}}E+{{E}^{T}}\frac{\partial {{C}^{-1}}}{\partial {{x}_{k}}}E+{{E}^{T}}{{C}^{-1}}\frac{\partial E}{\partial {{x}_{k}}} \right),\begin{matrix} {} & k=1,2,3 \\ \end{matrix}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial {{C}^{-1}}}{\partial {{x}_{k}}}C+{{C}^{-1}}\frac{\partial C}{\partial {{x}_{k}}}=0}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial U_{sys}^{ind}}{\partial {{x}_{k}}}=-\frac{1}{2}\frac{\partial {{E}^{T}}}{\partial {{x}_{k}}}{{\mu }^{ind}}+\frac{1}{2}{{E}^{T}}{{C}^{-1}}\frac{\partial C}{\partial {{x}_{k}}}{{C}^{-1}}E-\frac{1}{2}{{\left( {{\mu }^{ind}} \right)}^{T}}\frac{\partial E}{\partial {{x}_{k}}}}

Define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle M^t=M^{perm} + M^{ind}}

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =-{{\left( {{\mu }^{ind}} \right)}^{T}}\frac{\partial {{T}^{1}}M}{\partial {{x}_{k}}}-\frac{1}{2}{{\left( {{\mu }^{ind}} \right)}^{T}}\frac{\partial {{T}^{11}}}{\partial {{x}_{k}}}{{\mu }^{ind}}}

The above is in addition to the permanent ele forces (second term is related to torque, which can be converted to forces on frame defining atoms).

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial U_{sys}^{t}}{\partial {{x}_{k}}}=-\frac{1}{2}{{\left( {{M}^{t}} \right)}^{T}}\frac{\partial {{T}^{1}}}{\partial {{x}_{k}}}{{M}^{t}}-{{\left( {{M}^{t}} \right)}^{T}}{{T}^{1}}\frac{\partial \Re }{\partial {{x}_{k}}}{{M}^{{}}}}